15.7 Surface Integrals and Flux by SGLee, 이원준

 (Ref. http://math1.skku.ac.kr/home/pub/1884/ 2013.12.11)
(Ref. http://math1.skku.ac.kr/home/pub/1884/ 2013.12.11)
Surface integrals of scalar fields
To find an explicit formula for the surface integral, we need to parameterize the surface of interest, S, by considering a system ofcurvilinear coordinates on S, like the latitude and longitude on a sphere. Let such a parameterization be x(s, t), where (s, t) varies in some region T in the plane. Then, the surface integral is given by
where the expression between bars on the right-hand side is the magnitude of the cross product of the partial derivatives of x(s, t), and is known as the surface element.
Surface integrals of vector fields
Consider a vector field v on S, that is, for each x in S, v(x) is a vector.
The surface integral can be defined component-wise according to the definition of the surface integral of a scalar field; the result is a vector. This applies for example in the expression of the electric field at some fixed point due to an electrically charged surface, or the gravity at some fixed point due to a sheet of material.
Alternatively, if we integrate the normal component of the vector field, the result is a scalar. Imagine that we have a fluid flowing through S, such that v(x) determines the velocity of the fluid at x. The flux is defined as the quantity of fluid flowing through S in unit amount of time.
This illustration implies that if the vector field is tangent to S at each point, then the flux is zero, because the fluid just flows inparallel to S, and neither in nor out. This also implies that if v does not just flow along S, that is, if v has both a tangential and a normal component, then only the normal component contributes to the flux. Based on this reasoning, to find the flux, we need to take the dot product of v with the unit surface normal to S at each point, which will give us a scalar field, and integrate the obtained field as above. We find the formula
The cross product on the right-hand side of this expression is a surface normal determined by the parametrization.
(Ref. http://en.wikipedia.org/wiki/Surface_integral 2013.12.11)
![]()
1.Evaluate the surface integral ![]() , where
, where ![]() is the surface defined by the vector function
is the surface defined by the vector function ![]() , where
, where ![]() ,
, ![]() .
.
![]()
The graph of ![]() is called sphere.
is called sphere.
Substituting ![]() ,
, ![]() and
and ![]() into the integrand and we have
into the integrand and we have
![]()
![]() .
.
![]() and
and
![]()
![]()
![]()
![]()
![]() .
.
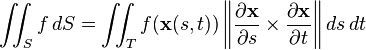

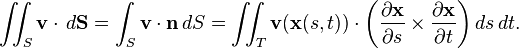
 .
.





