■
(Citation : Jin Ho Kwak and Sungpyo Hong, 1997, Linear Algebra, 335p)
Additional Information
jordan form을 이용한 미분방정식의 풀이는 임의의 행렬  에 대해서 가능하다.
에 대해서 가능하다.
그와 다르게 임의의 대각화 가능한 행렬  에 대해서는 보다 간단한 다른 풀이를 할 수 있다.
에 대해서는 보다 간단한 다른 풀이를 할 수 있다.

* 행렬의 대각화를 이용한 미분방정식의 해
성대 이상구 교수
자연과학과 공학의 많은 문제들은 다음과 같은 일계 미분방정식들의 연립방정식을 푸는 수학적 문제로 바꿀 수 있다.
 (1)
(1)
여기서,  이다.
이다.
방정식 (1)의 해는  축의 임의의 구간에서 정의된 모든
축의 임의의 구간에서 정의된 모든  에 대하여 방정식 (1)을 만족하는 모든 미분가능한 함수들의
에 대하여 방정식 (1)을 만족하는 모든 미분가능한 함수들의  개의 순서조 (
개의 순서조 ( ) 이다.
) 이다.
이 절에서는 식 (1)의 계수행렬  가 대각화가능한 경우에 행렬의 대각화를 이용하여 연립방정식을 푸는 방법에 대하여 알아본다.
가 대각화가능한 경우에 행렬의 대각화를 이용하여 연립방정식을 푸는 방법에 대하여 알아본다.  가 대각화가능하지 않은 경우는 Jordan표준형을 이용하여 해를 구할 수 있다. Jordan표준형은 8.4절에서 다룬다.
가 대각화가능하지 않은 경우는 Jordan표준형을 이용하여 해를 구할 수 있다. Jordan표준형은 8.4절에서 다룬다.
 이라 하면
이라 하면 이므로
이므로
 (2)
(2)
로 쓸 수 있다. 식 (2)의 가장 단순한 형태는  가 대각행렬
가 대각행렬

인 경우이다. 이 경우  는 독립적인
는 독립적인  개의 연립방정식들로, 다음과 같이 나타내어진다.
개의 연립방정식들로, 다음과 같이 나타내어진다.
 (3)
(3)
여기서  번째의 방정식인
번째의 방정식인  의 일반해는
의 일반해는  (
( 는 임의 상수)이므로 방정식 (3)의 일반해는 다음과 같음을 알 수 있다.
는 임의 상수)이므로 방정식 (3)의 일반해는 다음과 같음을 알 수 있다.
 (4)
(4)
이제, 계수행렬  가 대각화가능할 때, 이러한 과정이 어떻게 이루어지는지 살펴보자. 정리 6.1에서 보았드시
가 대각화가능할 때, 이러한 과정이 어떻게 이루어지는지 살펴보자. 정리 6.1에서 보았드시  가 대각화가능할 필요충분조건은
가 대각화가능할 필요충분조건은  가 자신의 고유값
가 자신의 고유값  에 대응하는
에 대응하는  개의 일차독립인 고유벡터
개의 일차독립인 고유벡터 을 갖는것이다. 이 때
을 갖는것이다. 이 때
 ,
, 
이라 하면  이므로
이므로  이고,
이고, 로 치환하면
로 치환하면  의 원소들은 상수이므로
의 원소들은 상수이므로  이다. 따라서 식 (5)로부터
이다. 따라서 식 (5)로부터

이고, 다음과 같이 계수행렬이 대각행렬인 새로운 연립미분방정식을 얻는다.
 (6)
(6)
따라서 식 (6)의 일반해는 식(4)와 같이

이다. 그런데  이므로 원래의 미분방정식
이므로 원래의 미분방정식 의 일반해는
의 일반해는

이다. 즉,
 (7)
(7)
이상으로부터 다음 정리를 얻는다.
정리 6.8 대각화가능한  차의 정사각행렬
차의 정사각행렬  의 고유값
의 고유값  에 대응하는 일차독립인 고유벡터를 각각
에 대응하는 일차독립인 고유벡터를 각각  이라고 하자. 그러면
이라고 하자. 그러면 의 해는 다음과 같다.
의 해는 다음과 같다.

【예제 2】 초기조건  을 갖는 다음 연립미분방정식의 해를 구하라.
을 갖는 다음 연립미분방정식의 해를 구하라.
 (8)
(8)
풀 이 계수행렬

의 고유값은  이고, 이에 대응하는
이고, 이에 대응하는  의 일차독립인 고유벡터로 각각
의 일차독립인 고유벡터로 각각
 ,
, 
를 얻을 수 있다. 따라서 정리 6.8에 의하여 이 미분방정식의 일반해는
 즉,
즉,


여기에  을 대입하여
을 대입하여  를 구하면
를 구하면  이다. 따라서, 식 (8)의 해는 다음과 같다.
이다. 따라서, 식 (8)의 해는 다음과 같다.
 ¶
¶
【예제 3】 다음 연립미분방정식을 풀어라
 (9)
(9)
풀 이 계수행렬

의 고유값은  이고, 이에 대응하는
이고, 이에 대응하는  의 일차독립인 고 유벡터로 각각
의 일차독립인 고 유벡터로 각각

를 얻을 수 있다. 따라서 일반해는 다음과 같다.


일반적으로, 상수계수를 갖는  계 선형미분방정식
계 선형미분방정식
 (10)
(10)
에서

로 치환하면, 선형미분방정식 (10)을 연립미분방정식 로 변환할 수 있다. 여기서, 계수행렬
로 변환할 수 있다. 여기서, 계수행렬 와 벡터
와 벡터 는 다음과 같다.
는 다음과 같다.
 ,
, 
【참 고】위의 행렬  를 다항식
를 다항식  의 동반행렬 (Companion matrix) 이라 한다. 행렬
의 동반행렬 (Companion matrix) 이라 한다. 행렬  의 특성 방정식은 바로
의 특성 방정식은 바로
 이다. 또, 위의 다항식 같이 최고차항의 계수가 1인 다항식을 모닉(monic)다항식이라고 한다.
이다. 또, 위의 다항식 같이 최고차항의 계수가 1인 다항식을 모닉(monic)다항식이라고 한다.
【예제 4】 다음 미분방정식을 풀어라
 (11)
(11)
풀 이 계수행렬

의 고유값은  이므로
이므로  는 대각화가능하고, 이러한 고유값에 대응하는
는 대각화가능하고, 이러한 고유값에 대응하는  의 일차독립인 고유벡터로 각각
의 일차독립인 고유벡터로 각각

를 얻을 수 있다. 따라서  에 대하여
에 대하여 의 일반해는 정리 6.8에 의하여
의 일반해는 정리 6.8에 의하여

이고, 식 (11)의 일반해는  이므로 다음과 같다.
이므로 다음과 같다.
 ¶
¶
(Citation : 이상구, http://matrix.skku.ac.kr/nla/ODE2/ODE2.htm, 2013.11.25)
선형 미분방정식 y가 실수일 때 ay''+by'+cy=0를 푸는 프로그램도 있다.
선형 미분 방정식 풀이 : http://matrix.skku.ac.kr/sglee/skku-java-out/single_diff.html (이상구, 2013.11.25에 인용)
연립 선형 미분 방정식 x'=ax+by, y'=cx+dy를 푸는 프로그램도 존재한다. 즉, 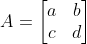 인 경우다.
인 경우다.
연립 선형 미분 방정식 풀이 : http://matrix.skku.ac.kr/sglee/skku-java-out/second_diff.html (이상구, 2013.11.25에 인용)
References
Jin Ho Kwak and Sungpyo Hong, 1997, Linear Algebra, 335-336p
이상구, 행렬의 대각화를 이용한 미분방정식의 해 : http://matrix.skku.ac.kr/nla/ODE2/ODE2.htm, 2013.11.25
MT 김신휘 Computation of e^A using Jordan Canonical Form : Link
SKKU Matrix Theory Contents
Back to the Index Page
with the initial condition
, where
,
.
with initial condition
is
. ( Ref. Jin Ho Kwak and Sungpyo Hong, 1997, Linear Algebra, 230-238p )
.
where
: the number of jordan blocks.
be natural numbers such that
is a
matrix.
( Ref. MT 김신휘 Computation of e^A using Jordan Canonical Form : Link )
where
and
.
인
의 Jordan form
와 transition matrix
를 구하자.

 (1)
(1) 이다.
이다. 축의 임의의 구간에서 정의된 모든
축의 임의의 구간에서 정의된 모든  에 대하여 방정식 (1)을 만족하는 모든 미분가능한 함수들의
에 대하여 방정식 (1)을 만족하는 모든 미분가능한 함수들의  개의 순서조 (
개의 순서조 ( ) 이다.
) 이다. 가 대각화가능한 경우에 행렬의 대각화를 이용하여 연립방정식을 푸는 방법에 대하여 알아본다.
가 대각화가능한 경우에 행렬의 대각화를 이용하여 연립방정식을 푸는 방법에 대하여 알아본다.  가 대각화가능하지 않은 경우는 Jordan표준형을 이용하여 해를 구할 수 있다. Jordan표준형은 8.4절에서 다룬다.
가 대각화가능하지 않은 경우는 Jordan표준형을 이용하여 해를 구할 수 있다. Jordan표준형은 8.4절에서 다룬다. 이라 하면
이라 하면 이므로
이므로 (2)
(2) 가 대각행렬
가 대각행렬
 는 독립적인
는 독립적인  개의 연립방정식들로, 다음과 같이 나타내어진다.
개의 연립방정식들로, 다음과 같이 나타내어진다. (3)
(3) 번째의 방정식인
번째의 방정식인  의 일반해는
의 일반해는  (
( 는 임의 상수)이므로 방정식 (3)의 일반해는 다음과 같음을 알 수 있다.
는 임의 상수)이므로 방정식 (3)의 일반해는 다음과 같음을 알 수 있다. (4)
(4) 가 대각화가능할 때, 이러한 과정이 어떻게 이루어지는지 살펴보자. 정리 6.1에서 보았드시
가 대각화가능할 때, 이러한 과정이 어떻게 이루어지는지 살펴보자. 정리 6.1에서 보았드시  가 대각화가능할 필요충분조건은
가 대각화가능할 필요충분조건은  가 자신의 고유값
가 자신의 고유값  에 대응하는
에 대응하는  개의 일차독립인 고유벡터
개의 일차독립인 고유벡터 을 갖는것이다. 이 때
을 갖는것이다. 이 때 ,
, 
 이므로
이므로  이고,
이고, 로 치환하면
로 치환하면  의 원소들은 상수이므로
의 원소들은 상수이므로  이다. 따라서 식 (5)로부터
이다. 따라서 식 (5)로부터
 (6)
(6)
 이므로 원래의 미분방정식
이므로 원래의 미분방정식 의 일반해는
의 일반해는
 (7)
(7) 차의 정사각행렬
차의 정사각행렬  의 고유값
의 고유값  에 대응하는 일차독립인 고유벡터를 각각
에 대응하는 일차독립인 고유벡터를 각각  이라고 하자. 그러면
이라고 하자. 그러면 의 해는 다음과 같다.
의 해는 다음과 같다.
 을 갖는 다음 연립미분방정식의 해를 구하라.
을 갖는 다음 연립미분방정식의 해를 구하라. (8)
(8)
 이고, 이에 대응하는
이고, 이에 대응하는  의 일차독립인 고유벡터로 각각
의 일차독립인 고유벡터로 각각 ,
, 
 즉,
즉,

 을 대입하여
을 대입하여  를 구하면
를 구하면  이다. 따라서, 식 (8)의 해는 다음과 같다.
이다. 따라서, 식 (8)의 해는 다음과 같다. ¶
¶ (9)
(9)
 이고, 이에 대응하는
이고, 이에 대응하는  의 일차독립인 고 유벡터로 각각
의 일차독립인 고 유벡터로 각각


 계 선형미분방정식
계 선형미분방정식 (10)
(10)
 로 변환할 수 있다. 여기서, 계수행렬
로 변환할 수 있다. 여기서, 계수행렬 와 벡터
와 벡터 는 다음과 같다.
는 다음과 같다. ,
, 
 를 다항식
를 다항식  의 동반행렬 (Companion matrix) 이라 한다. 행렬
의 동반행렬 (Companion matrix) 이라 한다. 행렬  의 특성 방정식은 바로
의 특성 방정식은 바로 이다. 또, 위의 다항식 같이 최고차항의 계수가 1인 다항식을 모닉(monic)다항식이라고 한다.
이다. 또, 위의 다항식 같이 최고차항의 계수가 1인 다항식을 모닉(monic)다항식이라고 한다. (11)
(11)
 이므로
이므로  는 대각화가능하고, 이러한 고유값에 대응하는
는 대각화가능하고, 이러한 고유값에 대응하는  의 일차독립인 고유벡터로 각각
의 일차독립인 고유벡터로 각각
 에 대하여
에 대하여 의 일반해는 정리 6.8에 의하여
의 일반해는 정리 6.8에 의하여
 이므로 다음과 같다.
이므로 다음과 같다. ¶
¶